from sklearn.datasets import load_breast_cancer

現在，下面的命令將加載數據集。

data = load_breast_cancer()

下面是一個重要的字典鍵列表−

• Classification label names(target_names)
• The actual labels(target)
• The attribute/feature names(feature_names)
• The attribute (data)

現在，藉助下面的命令，我們可以爲每個重要的信息集創建新變量並分配數據。換言之，我們可以使用以下命令組織數據−

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

現在，爲了使它更清晰，我們可以使用以下命令列印類標籤、第一個數據實例的標籤、我們的特徵名稱和特徵值;

print(label_names)

上面的命令將分別列印惡性和良性的類名。它顯示爲下面的輸出&負;

['malignant' 'benign']

現在，下面的命令將顯示它們映射到二進位值0和1。這裡0代表惡性腫瘤，1代表良性腫瘤。您將收到以下輸出&負;

print(labels[0])
0

下面給出的兩個命令將生成特徵名稱和特徵值。

print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

從上面的輸出可以看出，第一個數據實例是一個半徑爲1.799萬E+01的惡性腫瘤。

Step 3 − Organizing data into sets

在這一步中，我們將把數據分爲兩部分，即訓練集和測試集。把數據分成這些集合是非常重要的，因爲我們必須在看不見的數據上測試我們的模型。要將數據分割成多個集合，sklearn有一個函數，名爲train_test_split（）函數。藉助以下命令，我們可以拆分這些集合中的數據;

from sklearn.model_selection import train_test_split

上面的命令將從sklearn導入train_test_split功能，下面的命令將數據分成訓練和測試數據。在下面給出的示例中，我們使用40%的數據進行測試，其餘數據將用於培訓模型。

train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)

Step 4 − Building the model

在這一步，我們將建立我們的模型。我們將使用樸素的貝葉斯算法來建立模型。以下命令可用於構建模型−

from sklearn.naive_bayes import GaussianNB

上面的命令將導入GaussianNB模塊。現在，下面的命令將幫助您初始化模型。

gnb = GaussianNB()

我們將通過使用gnb.fit（）將模型與數據擬合來訓練模型。

model = gnb.fit(train, train_labels)

Step 5 − Evaluating the model and its accuracy

在這一步中，我們將通過對測試數據進行預測來評估模型。然後我們也會發現它的準確性。爲了進行預測，我們將使用predict（）函數。下面的命令將幫助您執行此操作;

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

以上0和1的序列是腫瘤級別的預測值-惡性和良性。

現在，通過比較test_labels和preds這兩個數組，我們可以發現模型的準確性。我們將使用accurity_score（）函數來確定精度。考慮下面的命令;

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

結果表明，NaïveBayes分類器的準確率爲95.17%。

這樣，通過以上步驟的幫助，我們可以用Python構建分類器。

Building Classifier in Python

在本節中，我們將學習如何用Python構建分類器。

Naïve Bayes Classifier

樸素貝葉斯是一種利用貝葉斯定理建立分類器的分類技術。假設預測值是獨立的。簡單地說，它假設類中某個特性的存在與任何其他特性的存在無關。爲了構建天真的Bayes分類器，我們需要使用名爲scikit learn的python庫。scikit學習軟體包中有三種樸素的Bayes模型，分別是高斯型、多項式型和伯努利型。

爲了建立一個樸素的Bayes機器學習分類器模型，我們需要

Dataset

我們將使用名爲威斯康星州乳腺癌診斷資料庫的數據集。該數據集包含有關乳腺癌的各種信息，以及惡性或良性的分類標籤。該數據集有569個腫瘤實例或數據，包括30個屬性或特徵的信息，如腫瘤半徑、紋理、平滑度和面積。我們可以從sklearn包導入此數據集。

Naïve Bayes Model

爲了建立樸素貝葉斯分類器，我們需要樸素貝葉斯模型。如前所述，scikit learn包下有三種類型的樸素Bayes模型，分別是高斯型、多項式型和伯努利型。在下面的例子中，我們將使用高斯樸素貝葉斯模型。

利用上述方法，我們將建立一個樸素的Bayes機器學習模型，利用腫瘤信息來預測腫瘤是惡性的還是良性的。

首先，我們需要安裝sklearn模塊。它可以在以下命令的幫助下完成−

Import Sklearn

現在，我們需要導入名爲「威斯康星州乳腺癌診斷資料庫」的數據集。

from sklearn.datasets import load_breast_cancer

現在，下面的命令將加載數據集。

data = load_breast_cancer()

數據可以按以下方式組織&負;

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

現在，爲了使它更清晰，我們可以使用以下命令列印類標籤、第一個數據實例的標籤、功能名稱和功能值;

print(label_names)

上面的命令將分別列印惡性和良性的類名。它顯示爲下面的輸出&負;

['malignant' 'benign']

現在，下面給出的命令將顯示它們映射到二進位值0和1。這裡0代表惡性腫瘤，1代表良性腫瘤。它顯示爲下面的輸出&負;

print(labels[0])
0

以下兩個命令將生成要素名稱和要素值。

print(feature_names[0])
mean radius
print(features[0])

[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

從上面的輸出可以看出，第一個數據實例是一個主要半徑爲1.799萬E+01的惡性腫瘤。

爲了在看不見的數據上測試我們的模型，我們需要將數據分成訓練和測試數據。它可以通過以下代碼來完成−

from sklearn.model_selection import train_test_split

上面的命令將從sklearn導入train_test_split功能，下面的命令將數據分成訓練和測試數據。在下面的例子中，我們將使用40%的數據進行測試，而remining數據將用於培訓模型。

train, test, train_labels, test_labels = 
train_test_split(features,labels,test_size = 0.40, random_state = 42)

現在，我們使用以下命令構建模型−

from sklearn.naive_bayes import GaussianNB

上述命令將導入GaussianNB模塊。現在，使用下面給出的命令，我們需要初始化模型。

gnb = GaussianNB()

我們將通過使用gnb.fit（）將模型與數據擬合來訓練模型。

model = gnb.fit(train, train_labels)

現在，通過對測試數據進行預測來對模型進行評估，可以做如下的工作;

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

上述0和1的序列是腫瘤級別（即惡性）的預測值

現在，通過比較兩個數組，即test_labels和preds，我們可以找出

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

結果表明，NaïveBayes分類器的準確率爲95.17%。

這就是基於樸素貝葉斯高斯模型的機器學習分類器。

Support Vector Machines (SVM)

基本上，支持向量機（SVM）是一種有監督的機器學習算法

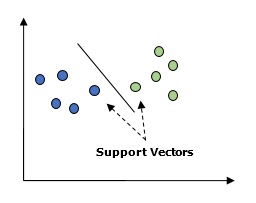
在上圖中，我們有兩個特性。因此，我們首先需要繪製這兩個

在這裡，我們將使用scikit學習和iris數據集構建一個支持向量機分類器。科學知識

Dataset

我們將使用iris數據集，它包含3個類，每個類50個實例，其中每個類都指iris植物的一種類型。每個實例都有四個特徵，即萼片長度、萼片寬度、花瓣長度和花瓣寬度。基於4個特徵預測虹膜植物分類的支持向量機分類器如下所示。

Kernel

這是支持向量機使用的一種技術。基本上，這些函數接受低維輸入空間並將其轉換爲高維空間。它將不可分問題轉化爲可分問題。核函數可以是線性、多項式、rbf和sigmoid中的任意一個。在這個例子中，我們將使用線性核。

現在讓我們進口下列包裹;

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

現在，加載輸入數據;

iris = datasets.load_iris()

我們採用前兩個特徵&負;

X = iris.data[:, :2]
y = iris.target

我們將用原始數據繪製支持向量機的邊界。我們正在創建一個要繪製的網格。

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

我們需要給出正則化參數的值。

C = 1.0

我們需要創建SVM分類器對象。

Svc_classifier = svm_classifier.SVC(kernel='linear', 
C=C, decision_function_shape = 'ovr').fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize = (15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')

Logistic Regression

基本上，logistic回歸模型是監督分類算法家族的成員之一。Logistic回歸通過使用Logistic函數估計機率來度量因變量和自變量之間的關係。

這裡，如果我們討論因變量和自變量，則因變量是我們要預測的目標類變量，而另一方面，自變量是我們要用來預測目標類的特徵。

在logistic回歸中，估計機率意味著預測事件發生的可能性。例如，店主希望預測進入商店的客戶是否會購買play station（例如）。店主會觀察到顧客的許多特徵，如性別、年齡等，以預測發生的可能性，即是否購買一個娛樂站。logistic函數是用來建立各種參數函數的乙狀結腸曲線。

Prerequisites

在使用logistic回歸構建分類器之前，我們需要在系統上安裝Tkinter包。它可以從https://docs.python.org/2/library/tkinter.html安裝。

現在，藉助下面給出的代碼，我們可以使用logistic回歸創建一個分類器;

首先，我們將進口一些包裝;

import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

現在，我們需要定義示例數據，這些數據可以如下所示−

X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
              [3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])

接下來，我們需要創建logistic回歸分類器，其操作如下所示;

Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)

最後但並非最不重要的是，我們需要訓練這個分類器;

Classifier_LR.fit(X, y)

現在，我們如何可視化輸出？它可以通過創建名爲Logistic_visualize（）−的函數來完成;

Def Logistic_visualize(Classifier_LR, X, y):
   min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
   min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0

在上面的行中，我們定義了網格網格中使用的最小值和最大值X和Y。此外，我們將定義繪製網格網格的步長。

mesh_step_size = 0.02

讓我們定義X和Y值的網格網格，如下所示;

x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size),
                 np.arange(min_y, max_y, mesh_step_size))

藉助以下代碼，我們可以在網格網格上運行分類器−

output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
output = output.reshape(x_vals.shape)
plt.figure()
plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray)
 
plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black', 
linewidth=1, cmap = plt.cm.Paired)

下面的代碼行將指定繪圖的邊界

plt.xlim(x_vals.min(), x_vals.max())
plt.ylim(y_vals.min(), y_vals.max())
plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0)))
plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0)))
plt.show()

現在，在運行代碼之後，我們將得到以下輸出，logistic回歸分類器−

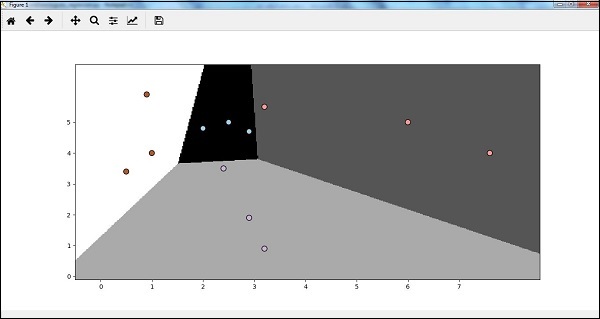
Decision Tree Classifier

決策樹基本上是一個二叉樹流程圖，每個節點根據某個特徵變量分割一組觀測值。

在這裡，我們正在建立一個預測男性或女性的決策樹分類器。我們將採集一個非常小的數據集，有19個樣本。這些樣本包括兩個特徵——「身高」和「頭髮長度」。

Prerequisite

爲了構建下面的分類器，我們需要安裝pydotplus和graphviz。基本上，graphviz是使用點文件繪製圖形的工具，而pydotplus是graphviz點語言的模塊。它可以與包管理器或pip一起安裝。

現在，我們可以藉助以下Python代碼構建決策樹分類器−

首先，讓我們導入一些重要的庫，如下所示;

import pydotplus
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn import cross_validation
import collections

現在，我們需要提供以下數據集&負;

X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32],
[166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38],
[169,9],[171,36],[116,25],[196,25]]

Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman',
'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man']
data_feature_names = ['height','length of hair']

X_train, X_test, Y_train, Y_test = cross_validation.train_test_split
(X, Y, test_size=0.40, random_state=5)

在提供數據集之後，我們需要對模型進行擬合，具體操作如下所示;

clf = tree.DecisionTreeClassifier()
clf = clf.fit(X,Y)

可以藉助以下Python代碼進行預測−

prediction = clf.predict([[133,37]])
print(prediction)

藉助以下Python代碼，我們可以可視化決策樹;

dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
            out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)

for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))

for edge in edges: edges[edge].sort()

for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('Decisiontree16.png')

它將上述代碼的預測值設爲['Woman']，並創建以下決策樹−

我們可以在預測中改變特徵值來測試它。

Random Forest Classifier

我們知道，集成方法是將機器學習模型組合成更強大的機器學習模型的方法。隨機森林，決策樹的集合，就是其中之一。它優於單一決策樹，因爲它在保持預測能力的同時，可以通過對結果進行平均來減少過度擬合。在這裡，我們將在scikit-learn癌症數據集上實現隨機森林模型。

進口必要的包裝;

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
import matplotlib.pyplot as plt
import numpy as np

現在，我們需要提供以下數據集

cancer = load_breast_cancer()
X_train, X_test, y_train,
y_test = train_test_split(cancer.data, cancer.target, random_state = 0)

在提供數據集之後，我們需要對模型進行擬合，具體操作如下所示;

forest = RandomForestClassifier(n_estimators = 50, random_state = 0)
forest.fit(X_train,y_train)

現在，得到訓練和測試子集的精度：如果我們增加估計量的數量，測試子集的精度也會提高。

print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train)))
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))

Output

Accuracy on the training subset:(:.3f) 1.0
Accuracy on the training subset:(:.3f) 0.965034965034965

現在，與決策樹一樣，random forest也有了特徵重要性模塊，這將提供比決策樹更好的特徵權重視圖。它可以按如下方式繪製和可視化;

n_features = cancer.data.shape[1]
plt.barh(range(n_features),forest.feature_importances_, align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.show()

Performance of a classifier

在實現了機器學習算法之後，我們需要找出模型的有效性。衡量有效性的標準可以基於數據集和度量。爲了評估不同的機器學習算法，我們可以使用不同的性能指標。例如，假設使用一個分類器來區分不同對象的圖像，我們可以使用分類性能指標，如平均精度、AUC等。在某種意義上，我們選擇用來評估我們的機器學習模型的指標是非常重要的，因爲指標的選擇會影響機器學習模型的性能對機器學習算法進行了測試和比較。以下是一些度量標準;

Confusion Matrix

基本上它用於分類問題，其中輸出可以是兩個或更多類型的類。這是衡量分類器性能的最簡單方法。混淆矩陣基本上是一個具有「實際」和「預測」兩個維度的表。這兩個維度都有「真陽性（TP）」、「真陰性（TN）」、「假陽性（FP）」、「假陰性（FN）」。

在上面的混淆矩陣中，1表示正類，0表示負類。

以下是與混淆矩陣相關的術語;

• 當實際的數據點類別爲1而預測的數據點類別也爲1時，即爲真正TPs。

• 真負數是指數據點的實際類爲0，預測類也爲0的情況。

• 當數據點的實際類爲0，而預測類也爲1時，即爲誤報FPs。

• 假陰性−FNs是指數據點的實際類爲1，預測類也爲0的情況。

Accuracy

混淆矩陣本身並不是一種性能度量，但幾乎所有的性能矩陣都基於混淆矩陣。其中之一就是準確性。在分類問題中，它可以定義爲模型對所有類型的預測進行正確預測的次數。計算精度的公式如下所示;

$$Accuracy = \frac{TP+TN}{TP+FP+FN+TN}$$

Precision

它主要用於文檔檢索。它可以定義爲返回的文檔中有多少是正確的。以下是計算精度的公式;

$$Precision = \frac{TP}{TP+FP}$$

Recall or Sensitivity

它可以定義爲模型返回的正數。下面是計算模型的召回率/靈敏度的公式;

$$Recall = \frac{TP}{TP+FN}$$

Specificity

它可以定義爲模型返回的負片數量。這與回憶恰恰相反。下面是計算模型特異度的公式;

$$Specificity = \frac{TN}{TN+FP}$$

Class Imbalance Problem

類不平衡是指屬於一個類的觀察數明顯低於屬於其他類的觀察數的情況。例如，在需要識別罕見疾病、銀行欺詐交易等情況下，這個問題就顯得尤爲突出。

Example of imbalanced classes

讓我們以欺詐檢測數據集爲例來理解不平衡類的概念;

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

Solution

平衡類「可以解決不平衡類的問題。平衡階級的主要目的是增加少數階級的頻率，或者減少多數階級的頻率。以下是解決不平衡類問題的方法;

Re-Sampling

重採樣是一系列用於重建樣本數據集的方法，包括訓練集和測試集。爲了提高模型的精度，對模型進行了重採樣。以下是一些重採樣技術&負;

• 隨機欠採樣−此技術旨在通過隨機消除大多數類示例來平衡類分布。這是在多數和少數階級的情況得到平衡之前完成的。

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

在這種情況下，我們從非欺詐案例中抽取10%的樣本而不進行替換，然後將其與欺詐案例結合起來;

抽樣不足後的非欺詐性觀察=4950的10%=495

與欺詐性觀察相結合後的觀察總數=50+495=545

因此，現在，欠採樣後新數據集的事件率=9%

這種技術的主要優點是可以減少運行時間和提高存儲容量。但另一方面，它可以丟棄有用的信息，同時減少訓練數據樣本的數量。

• 隨機過抽樣−此技術旨在通過複製少數類中的實例數量來平衡類分布。

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

如果我們複製50個僞觀測值30次，那麼複製少數階級觀測值後的僞觀測值爲1500。過採樣後新數據中的總觀測值爲4950+1500=6450。因此，新數據集的事件率將爲1500/6450=23%。

這種方法的主要優點是不會丟失有用的信息。但另一方面，由於它複製了少數階級的事件，因此它有更大的機會過度擬合。

Ensemble Techniques

這種方法基本上是用來修改現有的分類算法，使它們適合於不平衡的數據集。在這種方法中，我們從原始數據中構造幾個兩級分類器，然後對它們的預測進行聚合。隨機森林分類器是基於集成的分類器的一個例子。